Printer-friendly version

TADA-Ed for Educational Data Mining
Agathe Merceron, Paris La Défense Cedex
Kalina Yacef, University of Sydney

Abstract
TADA-Ed stands for Tool for Advanced Data Analysis in Education. It is a data mining platform dedicated to teachers, allowing them to visualize and mine students on-line exercise work with the aim of discovering pedagogically relevant patterns. Most of the time, prior to mining, the data stored in a database needs some transformation. TADA-Ed contains pre-processing facilities so that users can transform the database tables to a format that, when used with a particular data mining algorithm, can generate meaningful results for the teacher. We show an application using students' mistakes recorded during exercises from a web-based tutoring tool.

About the authors...

1. Introduction
The internet brought important changes in many domains, including Education. Nowadays a large range of web-based applications support teaching and learning and comprise adaptive features requiring each user to log in. We are particularly interested in analysing the data recorded by such programs, such as students' interactions and answers, mistakes, teachers' comments and so on. This data can be stored in a database and mined to discover pedagogically relevant information. The aim of the tool TADA-Ed is to integrate various visualization and data mining facilities to help teachers in this discovering process. TADA-Ed stands for Tool for Advanced Data Analysis for Education.

To the best of our knowledge, there are very few tools dedicated at finding pedagogically relevant information in student work. Many tools solely produce statistics on marks, good and bad answers, or mistakes. The C.H.I.C. software [1] is a tool that produces more sophisticated information for teachers. It rests on implicative statistical analysis, an approach that we have not considered here and that produces other kinds of associations than the association rules algorithm included in TADA-Ed. The work by Bisson et al. [2] on the statistical analysis of students' behavior in algebra shows that valuable information can be extracted. They focus on the analysis of students' interactions with the system. Similarly, studies of web usage have been applied to eLearning [3]. CourseVis [4] is a quite sophisticated visualisation tool allowing teachers to explore student data. Our aim is to have a tool that can exploit students' interactions, web logs as well as data with richer semantic information such as the relevance of an action, the evaluation of correctness and, if applicable, the type of mistake made.

Of course, one may object that a number of excellent data mining platforms exists, commercially (such as [5]) as well as open source (such as [6]). However they are not tailored to the needs for Education. Firstly, these platforms are too complex for teachers and educators to use. Their features go well beyond the scope of what a teacher may want to do. Therefore the cognitive load associated with operating the program itself is too great to make them practical, as they reduce the users' cognitive resources to actually perform their task [7]. Secondly and most importantly, we found that the mining queries we wanted to run were not possible for the following reasons:

• From a data structure point of view, mining student data involves handling items that do not always have the same structure. For example, a student may do 5 exercises, with 4 mistakes, another may do 20 exercises with 10 mistakes. We still need to be able to compare them, although their activity is very different. Therefore we need enhanced preprocessing facilities that prepare the data in a meaningful and useful way.
• Also some algorithms may need to be tuned to take into account the educational context. For example, while practicing, students make mistakes that occur in some sequence. Some algorithms need to be adapted to take that sequentiality into account, or to ignore "old" data.
• Lastly, the display of the results needs to be meaningful to the teachers. We found that visualization offered by other tools is not always appropriate.

The paper is organized as follows. Section 2 presents the tool. In Section 3 we present examples of its features and of their use with student work obtained from a tool used in our undergraduate teaching. We have anonymised (i.e. give fictitious names) and simplified the data (i.e. we deleted some fine-grained information) and used generic terms so that the reader can understand the data without knowing the tool. Section 4 concludes the paper.

2. The Tool
In addition to visualization and data mining algorithms, TADA-Ed includes filtering and preprocessing facilities. Filtering is used to handle a sub-table of a database. Preprocessing is used to generate new tables in a format suitable for particular data mining algorithms.

2.1 General presentation
As can be seen in Figure 1, there are four main windows in TADA-Ed. The top left one, graph view, displays histograms and lines. The top right one, Points view, displays a 2 dimensional graph. A particularity of its implementation is that the x and y axis need not to be quantitative values (numbers); they may also be discrete values thus allowing to plot logins of students against mistakes made for example. A message log area is available on the left part of the screen to display various messages.

The bottom left frame contains classification and clustering algorithms (presently k-means, hierarchic clustering and decision trees). These three algorithms have been adapted from the open source Data Mining library Weka [6]. The aim of k-means and hierarchical clustering is to group elements that are similar according to some specific criteria defined by the user. The aim of a decision tree classifier is to classify an element with a subset of other elements. It may be used to predict the mark of a student with all the work stored in the database for instance.

These previous windows are linked together. The results of the k-means algorithm are displayed in the Points view window. Clicking a point (or a rectangle of points) in the Points view shows their attributes in the message area. Clicking a bar in the Graph View window colors the relevant points in the Points View window.

Figure 1. General overview of TADA-Ed

Overview of TADA: (Powerpoint, ~900 KB) animation showing all the windows and links between them.

The bottom right frame contains two association rules algorithms: the first one implements the classical A-priori algorithm [8] and the second one adapts the A-priori algorithm to take sequence into account. A typical use of the association algorithm is to identify mistakes that often come together. For example, if students make mistake A and mistake B, then they are likely to make mistake C, which we denote by A,B®C.

In our variant of A-priori which takes sequence into account, the rule A,B®C reads as follows: if students make mistake A, followed by mistake B, then later they make mistake C.

We also highlight that an Administration menu contains all the facilities related to the administration of the software: filters (selection of subset of data) and preprocessing of the database for the classification/clustering module and association rules module.

We explained that one of the particularities of TADA-Ed was its preprocessing functionalities. We will now describe them.

2.2 Preprocessing
Preprocessing allows the user to transform database tables to a format that transforms the selected data into a suitable shape to be used by a particular algorithm. Usually, in Data Mining tools, the transformation performed is a re-casting of the data, or the calculation of a new attribute from existing ones. For example, numerical attributes may be cast into nominal attributes. TADA-Ed goes further by providing six different kinds of transformations listed in Table 1.

Let us suppose the teacher wants to perform a clustering algorithm to group students according to the mistakes they made. The data may contain several entries for each student: one entry per mistake. For the clustering algorithm to work we need to gather these entries to form one single vector per student, so that these students can be "compared". The purpose of the preprocessing is to gather these entries per each value of a chosen attribute and to collect and transform information brought by the other attributes. The various types of preprocessing available in TADA-Ed are shown in Table 1. It is important to note that in TADA-Ed, each attribute can have a different preprocessing type. Some powerful data mining platforms offer some of these preprocessing features (nominal and total number) but apply them to all the attributes of the table.

Table 1. Preprocessing types

Overview of TADA: (Powerpoint, ~200 KB) animation explains precisely how each type of preprocessing works.

3 Application
We illustrate the use of our tool on data collected through a web-based tutoring tool used in undergraduate classes over 4 years. For the purpose of this paper, we simplified the data so that no specific knowledge of the way the tool works is required and we only describe the bare minimum of the data required to understand the paper. Students use the tool to do exercises, involving step-by-step answers and feedback. They can make mistakes, while using a particular concept.

We will illustrate the use of TADA-Ed through different mining experiments.

3.1 Unfinished exercises
With the tutoring tool we consider, an exercise is finished once the student has entered (eventually) all the correct steps until the solution was found. Therefore it might be interesting for teachers to explore what is the matter when students attempt exercises, make mistakes and do not finish them.

First, we will look at all the mistakes made by students in exercises that were never finished. For this we will use the "mistake" table, shown in Table 2, and filter it to only keep the lines where the finish date is empty. We get a sub-table of Mistake containing only the mistakes that were serious enough to prevent students from completing the exercise.

Table 2. Mistake table

Some examples of simple but useful visualisations for the teacher include the frequency of mistakes made, the concepts that were involved in the mistakes. These are shown in the figures below. In both figures, the teacher can select a bar (which is then highlighted in red) and the corresponding points are highlighted in red in the points view window (not shown). A message also appears in the message window indicating what has been selected. So here the mistake made the most often is M4, whilst the concept involving the most mistakes was C14.

We will now use k-means clustering to form groups of students. The aim is to create n-groups of students of homogeneous levels with respect to learning. There are several ways to achieve this goal. If one were interested in a global picture of all students, one would consider all students, their mistakes and their correct answers. As said above, we choose to focus on students who did not finish at least one exercise after making mistakes in their attempt. A sensible way to group these students in homogenous levels with respect to learning difficulties is to take into account the number of mistakes on concepts of the same class and the number of attempted exercises to perform k-means clustering.

• Creation of a higher granularity of concepts. The distinction of many different concepts is not always relevant for grouping students. We create a new attribute called "type of concept", which will combine the various 28 different concepts in 3 main sets called "simple1", "simple2", "complex2". TADA-Ed has a function called "Typology" which allows us to do that.
• Preprocessing. Then we need to prepare the data for the k-means, using the pre-processing facility. Since we want to group students, we choose to aggregate the data under the attribute login. Then out of all the attributes available, we decide to run the k-means using:
  • qid (Number of types): i.e., for each student, the number of exercises unfinished
  • mistake (Total number): i.e., for each student, the total number of mistakes made in unfinished exercises
  • type of concept (Nominal): i.e. for each student 3 binary values (simple1, simple2, complex2) flagging whether there are mistakes involving concepts for each group
  That way, two students who have not finished the same number of exercises, made the same number of mistakes involving similar types of concepts are "equal"; their distance is 0.

Figure 5. K-means preprocessing window

Full size image

• K-means algorithm. Once the data is ready to be processed, we start the k-means, asking for a maximum number of 5 clusters. As soon as the clusters are formed, they can be displayed in the Points View window, color-coded according to their cluster number, as shown in Figure 6. Their statistics can also be displayed, as shown in Figure 7.

Figure 7. Clustering statistics window

Full size image

After running the k-means algorithm, we obtain the five clusters displayed above. Group 0 is red, with 9 students. Group 1 is displayed in green and has 2 students. Group 2 is displayed in blue and has 10 students. Group 3 is displayed in yellow and has 20 students, and group 4 is displayed in purple and has 11 students. The y-axis gives the concept. The statistics window displays the characteristics of each cluster. For instance, here, the mean and standard deviation is indicated for qid and mistake, because the way these fields were preprocessed generated a numeric number. The window indicates for instance that cluster 1 made 25.5 mistakes in 5.5 exercises on average. For this type of concept, however, the statistics window shows, for each attribute, a percentage value. These values are color-coded depending on how they characterise the cluster. A red field means that the elements (students) of the cluster have that value present. A blue field means exactly the opposite, i.e., that the value is in general not present for the elements of the cluster. A black value (which is not shown here) means that the value is sometimes positive, sometimes negative, but not in significant amount to grant commonness between the elements. So at a glance, we can see that cluster 0 did not make any mistake involving simple1 type of concept (value is 0) and not much involving complex2 (value is 0.11), but they all made mistakes involving simple2 type of concepts. Whereas cluster 4 is characterised by making mistakes involving the three type of concepts.

Figure 6 shows an interesting cluster from a teacher's perspective, cluster 4 may need immediate action. Indeed, it contains students who have made mistakes with concepts in all classes, that have not attempted many exercises, 1.82 on average, but that have made the most mistakes 38.64 on average. Looking back at Figure 5, there is at least one concept that seems to be difficult for them, the one that draws an almost horizontal purple line. Almost all students from that group have made a mistake with that concept.

3.2 Classification/prediction of marks according to mistakes
In addition to the mistake table, we are now using another table which, among others, comprises the following attributes:

Table 3. Student_infos table

We joined the two tables and constructed a decision tree using as a common attribute the login of the student and preprocessed the data as follows:

• type of concept: Nominal
• mistake: Total number
• count_logins : Mean
• ex07: Mean

The tree is shown in Figure 8:

Figure 8. Decision tree result

Full size image

TADA-Ed displays the leaves of the tree with a coloring scheme reflecting the density of the leaf, which goes from grey (low density) to green (high density).

In addition, the login of each student appears at the bottom of the window, in a pop-up menu and by selecting one (here, Phil), its path is colored in red. So Phil is part of the group who made less than 9.5 mistakes (but more than 4.5) and who logged in less than 4.2 times. His exam mark was around 3.72 (out of 7).

This tree can now be saved and used to predict future marks. If bad marks are predicted from the tree, one may warn students. The path on the tree indicates how their work with the tool leads to the prediction. Students may reflect on that and take remedial actions.

3.3 Association rules
The goal of the association rules algorithm is to detect relationships or associations between specific values of nominal attributes in large data sets. For example, see our simple set of data shown in Figure 9. The first line indicates that if M1 and C3 are present in a line of the table, we can expect item M3 and C3 are also present with a support of 2.5%, a confidence of 54%, and a lift of 1.12. In other words, if a student makes mistake M1 with Concept C3 then s/he is likely to make mistake M3 with concept C3, with the support and confidence given. The support is an indicator of how many lines in the table are concerned by this association. The confidence is an indicator of the causality between the item(s) in the column item1 and the item(s) in the column item2. The lift is an indicator of the symmetric dependence between the item(s) in the column item1 and the item(s) in the column item2. A lift below 1 is usually considered as too low.

One use of the association algorithm is to identify mistakes that often come together. For example, we could point out that if students make mistake A and mistake B, then they also make mistake C, which we denote by A,B®C. A,B would belong to column item1, while C would belong to column item2 of Figure 9. The results of our use of the association rule in one of our teaching course is presented in [9]. The preprocessing tool for the association rules allows the user to choose more than one attribute to include in the A-priori algorithm. As a result, it would be possible to identify associations binding several attributes such as: mistakes A with concept X implies mistake B with concept Y, A&X®B&Y.

The association rules module implements the A-priori algorithm [8] that we modified in a number of variations to suit the educational context.

• First, we can search associations on one or two attributes, linked with an "AND" or an "OR". For instance Figure X shows the result of a query asking to search associations on mistakes and concepts.
• Second, the user can specify which attribute the data should be aggregated. If we chose login, it means that associations will be searched in sequences of mistakes per login. This means that associations will not be built when a user makes a mistake X and another user subsequently makes mistake Y.
• Thirdly, we can request that sequentiality be taken into account. This means that items are examined in sequence. Hence, if a mistake X is made before a mistake Y, the system will not count for the support of the association Y->X for instance.

Lastly we added an important feature to this module allowing the teacher to export some rules (in XML format) that can then be imported in a tutoring system to provide pro-active feedback to users [10].

4 Conclusion
TADA-Ed is a Data Mining tool that is designed to mine primarily data collected in an educational context. Therefore it includes Data Mining algorithms that provide sensible information for teachers. Presently, in addition to pre-processing facilities and various visualization graphs, it includes some classification and clustering algorithms, and association rule algorithms.

The tool is implemented and operational. We have illustrated several of its features using data coming from a real tutoring system. For instance, a combination of filtering and visualisation facilities allows us to see mistakes made by students who do not succeed in finishing exercises as well as concepts involved in these mistakes. Clustering facilities may lead to identifying interesting groups of students, like the group of students who make many mistakes with all sorts of concepts without attempting a significant number of exercises. Simple queries on data would not discover such a group. Another feature is to predict errors in the final exam and thus warn students who are likely to fail. We have used the tool to discover clustered mistakes, which lead us to reflect on the course material [9].

We are currently working to improve TADA-Ed. This first version provided us with some means to understand better which algorithms provide relevant information for teachers, which are the attributes to take into consideration and whether and how these algorithms need to be adapted. For example, student data has an important temporal link. This has led us to adapt the classical A-priori algorithm for association rules to take the order in which mistakes are made into account. This order is broader than usually understood, see [8], as it allows us to take into account the sequentiality between mistakes made while solving a single exercise as well as the sequentiality between mistakes done on exercises solved apart in time. Also importantly, educational data mining is now a growing research community and we expect that findings drawn from events such as [11, 12] will help us improve our work.

We also plan to tackle the interface to make it as easy as possible for teachers not too familiar with new technologies. This work will be carried out with researchers in Education. Whilst TADA-Ed in its current version can be used by a teacher who understands data mining, we need to make the tool accessible to any teacher who has a minimum of computer literacy. Finally, we would like to make the tool more intelligent, to save time for the teacher. Ideally, the tool would run automatically various Data Mining algorithms on the data and would alert the teacher when interesting/abnormal information has been discovered.

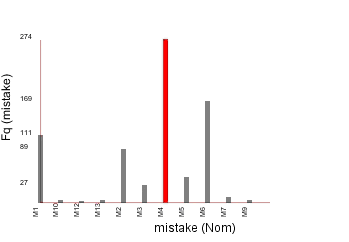
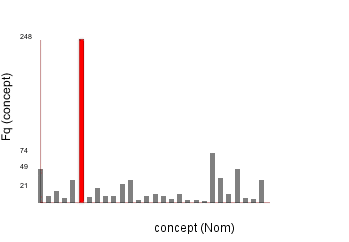
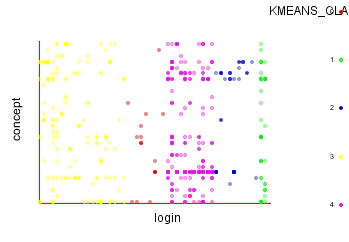
5. References
[1] CHIC, Logiciel d'analyse de données, www.ardm.asso.fr/CHIC.html (accessed 2003)

[2] Bisson, G., A. Bronne, M.B. Gordon, J.-F. Nicaud, & D. Renaudie. "Analyse statistique de comportements d'éléves en algébre" in Proceedings of EIAH2003 Environnements Informatiques pour l'Apprentissage Humain, Strasbourg, France: Paris: INRP (2003).

[3] Zaiane, O.R. "Web Usage Mining for a Better Web-Based Learning Environment" in Proceedings of Conference on Advanced Technology for Education (CATE'01), pp 60-64, Banff, Alberta (2001).

[4] Mazza, R. & V. Dimitrova. "CourseVis: Externalising Student Information to Facilitate Instructors in Distance Learning" in Proceedings of 11th International Conference on Artificial Intelligence in Education (AIED03), F. Verdejo and U. Hoppe (Eds), Sydney: IOS Press (2003).

[5] SPSS, Clementine, www.spss.com/clementine/ (accessed 2005)

[6] WEKA, www.cs.waikato.ac.nz/ml/weka (accessed 2003)

[7] Sweller, J., "Some cognitive processes and their consequences for the organisation and presentation of information". Australian Journal of Psychology. 45(1): p. 1-8 (1993).

[8] Agrawal, R. & R. Srikant. "Fast Algorithms for Mining Association Rules" in Proceedings of VLDB, Santiago, Chile (1994).

[9] Merceron, A. & K. Yacef. "A Web-based Tutoring Tool with Mining Facilities to Improve Learning and Teaching" in Proceedings of 11th International Conference on Artificial Intelligence in Education., F. Verdejo and U. Hoppe (Eds), pp 201-208, Sydney: IOS Press (2003).

[10] Merceron, A. & K. Yacef, "Educational Data Mining: a Case Study (paper accepted for the conference on Artificial Intelligence in Education, AIED2005)". Amsterdam, The Netherlands (2005).

[11] Beck, J., ed. Proceedings of ITS2004 workshop on Analyzing Student-Tutor Interaction Logs to Improve Educational Outcomes. Maceio, Brazil (2004).

[12] Choquet, C., V. Luengo, & K. Yacef, eds. Workshop on "Student usage analysis" to be held in conjunction with AIED 2005, Amsterdam, The Netherlands, July 2005. (2005).

6. Acknowledgements
The authors thank Valery Chhoa, Pascal Marchandeau and Morgan Cugerone for the improvements made to the tool.

********** End of Document **********

IMEJ multimedia team member assigned to this paper	Yue-Ling Wong