IMEJ main Wake Forest University Homepage Search articles Archived volumes Table of Content of this issue
1. Motivation
2. Environment
3. Adding Objects - A Simple Way
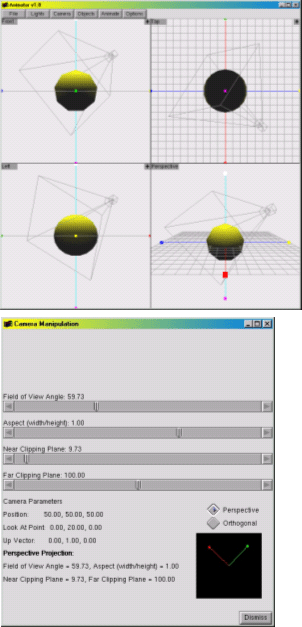
4. The Camera
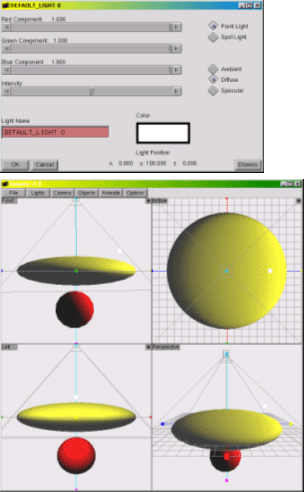
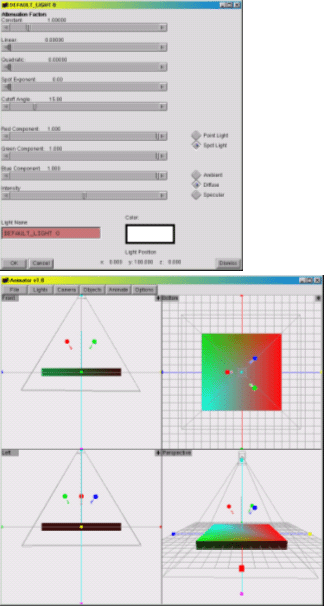
5. Lights, Please!
6. Basic Animation
7. Global Illumination Models
8. Future Work
9. Conclusions
10. Acknowledgment
11. References

Printer friendly version
Teaching and Learning Computer Graphics Made Easy with GraphicsMentor
Ching-Kuang Shene, Michigan Technological University

Abstract
The programming approach is perhaps the most popular approach in teaching introduction to computer graphics courses. However, it suffers a significant drawback. Students must learn a lot before they can write their first program. Worse, they may not even know if their images are correctly produced. Additionally, the programming approach depends on an API (e.g., OpenGL) that may only support local illumination models. Consequently, students will miss important topics that are associated with global illumination models. To overcome these problems, a pedagogical system GraphicsMentor was developed. GraphicsMentor allows students to modify parameters of the camera, objects, and light sources interactively, and visualize the rendered result on-the-fly. Moreover, it is able to export a scene to POV-Ray, a very popular ray tracing system, for rendering. GraphicsMentor is being extended to include photon mapping and radiosity. In this way, with the help of GraphicsMentor, a student should be able to grasp the fundamentals of computer graphics quickly and easily in a learning-by-doing way.

1. Motivation
The programming approach is perhaps the most popular approach in teaching introduction to computer graphics courses. However, the programming approach suffers a significant drawback in that students must learn a lot before they can write their first program. Even with tools designed by instructors helping students start programming early, students still face the challenge that in many situations they do not know if the generated results are correct. This is mainly due to the fact that to generate correct and good-looking images students must know many topics that can only be covered near the end of a semester. Consequently, their high hopes fade away quickly. Hoare once said, “You can't teach beginning programmers top-down design because they don't know which way is up.” Similarly, we cannot teach graphics programming to beginners because they do not know if their programs function properly before knowing what the anticipated effect would be. Thus, “I do and I understand'” (i.e., the programming approach) is not enough for learning graphics, and we should add “I see and I remember'' for a beginner to recognize what is correct and what is not. For example, the author’s experience shows that many students have difficulties in camera setup and the use of light sources. Frequently, a blank image is generated because the camera points to a wrong direction, or the scene is not illuminated properly because of incorrect positions of light sources. Moreover, they do not know if it is their fault when Mach bands appear in their images. Additionally, since graphics is not a prerequisite for our Introduction to Computing with Geometry course, we must cover sufficient graphics background so that students can write programs to solve geometric problems in curve and surface design (Lowther and Shene, 2001). Previously, we used ray tracing (Shene, 2002) because it is easy to learn and use; however, ray tracing only covers global illumination models and does not involve a programming component. We also believe that students must be exposed to local illumination models on which most API’s are based.

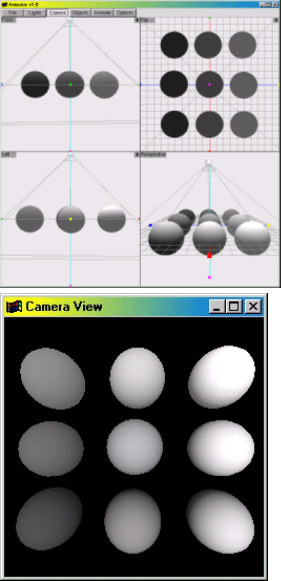
To address these and other problems, we developed GraphicsMentor, a pedagogical tool, written in C/C++, OpenGL and GLUT, for Linux, SGI IRIX, Sun Solaris, and Windows systems. It allows a student to alter virtually every parameter of the camera, light source and object material property, and visualize the result on-the-fly. A limited keyframe animation capability is also available. Because of its flexibility and interactive nature, GraphicsMentor can help students learn graphics fundamentals easily and quickly. Hence, GraphicsMentor may be used in a computer-equipped classroom or in a lab for students to practice and experiment with various concepts and for an instructor to demonstrate the effect of changing graphics parameters.

There are three major reasons for us to develop GraphicsMentor even though there are many high power systems available (e.g., trueSpace, LightWave 3D, 3D Studio Max and Maya) that support all features of GraphicsMentor. The first and the most important reason is cost. GraphicsMentor is designed to be pedagogical and is free for students and instructors to run on popular systems with minimal hardware requirement. Commercial professional systems cost a few hundred to several thousand dollars per copy and, as a result, they are not very cost effective. Worse, many of them can only function properly with a hardware lock in place, and the cost for a replacement if the lock is stolen is as high as purchasing a new copy. Second, due to its pedagogical nature, the use of GraphicsMentor is straightforward, whereas commercial professional systems usually have very steep learning curve because of their power and complex menu systems. Third, allowing students to redesign and/or modify various components of GraphicsMentor for supporting graphics programming has been one of our major goals. This support is similar to many pedagogical tools that are being used in other courses (e.g., Nachos for operating systems). However, such programming support is virtually impossible with commercial professional systems.

This paper briefly reviews GraphicsMentor and presents its possible classroom uses. The interested readers may refer to (Lowther and Shene, 2000; Lowther and Shene, 2001; Shene 2002) for a detailed discussion of related work.

2. The Environment
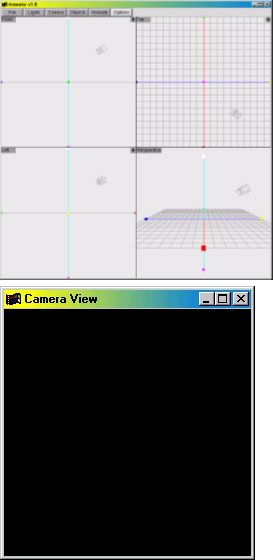
When GraphicsMentor starts, it displays the Canvas window and the Camera View window. The Canvas window is further divided into four subwindows (Figure 1(a)). The upper-left, upper-right, lower-left and lower-right subwindows display the front, top, left, and world views of the scene, respectively. The first three can be switched to the back, bottom, and right views by clicking on the button in the upper-left corner of each subwindow. Initially, the scene only contains a camera and a light source above the coordinate origin as shown by the camera icon and a white dot in the subwindows. 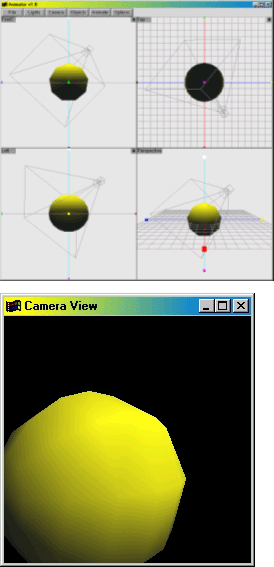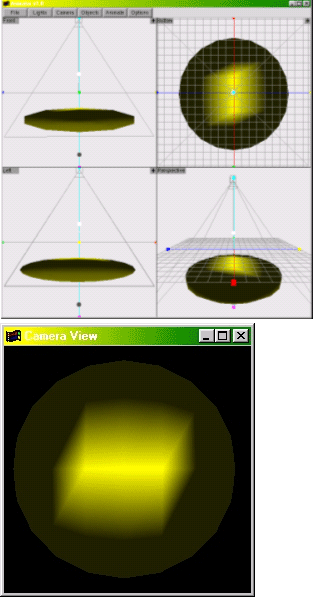The Canvas window also has a number of menu buttons for activating the camera, lights, objects and animation. The Camera View window displays what the camera sees (Figure 1(b)). Since nothing is in the scene initially, it shows the background color. With this setup, a student will have no difficulty in placing objects into the scene, manipulating the position of the camera, and changing the position, color, and type of light sources. Hence, the most challenging initial step of creating and viewing a scene is made much easier.

About the author...


Figure 1 (a) and (b). The Canvas and Camera View windows.

3. Adding Objects - A Simple Way
The first thing for a student to do is to add objects into the scene. GraphicsMentor supports six primitives (i.e., cube, pyramid, cylinder, cone, sphere and torus), although more complicated ones such as B-spline and NURBS surfaces will be added in the future. A click on the Objects menu button of the Canvas window brings up the Object List window (Figure 2(a)). The display area of the Object List window shows the default name of each object (e.g., OBJECT_1). Then, click on the New or Delete buttons for adding or removing an object, respectively. A click on the New button brings up the Object Modification window as shown in Figure 2(b). Click on one of the six buttons to display the corresponding object in the upper-left display area and on the canvas. Initially, these primitives have their default sizes, and a student may use the scaling slides to scale the object in the x-, y-, and z- directions.


Figure 2 (a) and (b). The Object List and Object Modification windows.


The default color of an object is always mid gray. The top four slides in the Object Modification window are used for changing the RGB color components and alpha channel, and this change can be applied to the ambient, diffuse, and specular components of the object's material property. The fifth slide is used for selecting the shininess of the object. Moreover, a student can left-drag and right-drag in the Canvas window to perform translation and trackball type rotation, respectively. With these capabilities, a student can quickly grasp the impact of different ambient and diffuse values on rendered shapes. In fact, it is easy to place a number of spheres in the scene, each of which has a different combination of ambient and diffuse values, and observe the differences among the rendered results. Figure 3 is such an example. The spheres on the first, second and third rows have ambient values 0.6, 0.4 and 0.2, and the spheres on the first, second and third columns have diffuse values 0.2, 0.5 and 0.8.

Figure 3. An ambient and diffuse experiment.

(a) Canvas view
(b) Camera view

All objects are triangulated. If the default triangulation is too coarse for a particular application, a student may use the tessellation slide, the last slide in the Object Modification window (Figure 2(b)), to set the level of tessellation. Figure 4 shows the impact of tessellation levels 7, 14 and 21 on the rendered result. Although the shapes are rendered with smooth (i.e., Gouraud) shading, the silhouettes of these shapes are still angular as shown in the figures. This is a drawback of using triangulation.

Figure 4. Tessellation levels.
(a) level 7
(b) level 14
(c) level 21

Therefore, with the capabilities supported by the Object Modification window, students can quickly and easily learn the meaning and impact of each component of an object's material property, the use of geometric transformations (i.e., scaling with slides and translations and rotations with mouse buttons), and the impact of tessellation level. As a result, they will be able to write programs and recognize problems with confidence.

4. The Camera
The camera is the most important item because no image can be produced without a camera. A click on the Camera menu button in the Canvas window displays all characteristics of the camera on the canvas (Figure 5(a)), and brings up the Camera Manipulation window (Figure 5(b)). All four subwindows on the canvas show the camera icon, look-at point and view volume. A student may left-click on one of the side-view subwindows to place the camera at that position, or left-drag to move the camera. A right-click changes the camera's default look-at point. With the Camera Manipulation window, a student can modify the view angle, aspect ratio, near and far clipping planes, and camera orientation. Moreover, a student can choose the perspective or orthogonal view. All viewing parameters are shown in the lower left portion of the Camera Manipulation window (Figure 5(b)).

 

 

Figure 5. Camera manipulation.
(a) Canvas
(b) The Camera Manipulation window


The first slide of the Camera Manipulation window is used for changing the view angle, which mimics zooming. The second slide is for changing the aspect ratio of the view volume; however, since the Camera View window has an aspect ratio of 1:1, altering the aspect ratio changes the aspect ratio of the view volume only and distorted objects may occur in the Camera View window. The last two slides are for changing the positions of the near and far clipping planes. GraphicsMentor does not allow these two planes to cross each other. To change camera orientation, a student may left-drag the two perpendicular (i.e., the right and up) vectors in the small window in the lower-right corner of the Camera Manipulation window. Figure 6(a) shows a view volume with the near clipping plane close to the camera. The far clipping plane cuts part of the sphere off; however, this cannot be seen because the front side is not transparent. If we move the near clipping plane towards the sphere as shown in Figure 7, the Camera View window shows a clipped sphere. Through the front hole, one can see that the back-end is also clipped.

Figure 6 (a) and (b). Before modifying the near clipping plane.

Figure 7 (a) and (b). After modifying the near clipping plane.

With GraphicsMentor's detailed information and interactive capability, a student is able to learn and see the impact of all viewing related parameters without writing any program. In our experience, placing the camera at a position with proper orientation, and the correct use of the look-at point, view angle, and clipping planes could be very challenging to beginners, especially to those who do not have extensive experience in playing with cameras and camcorders. As we all know, many students generate blank screens! Fortunately, GraphicsMentor virtually eliminates this problem by providing students with an environment to practice and experiment with the effect of camera related parameters.

5. Lights, Please!
Being just as important as the camera, light sources illuminate the scene. GraphicsMentor supports a maximum of eight lights. GraphicsMentor includes only one initial active light whose position is above the coordinate origin. A click on the Lights menu button of the Canvas window brings up the Light List window in which all created lights are shown along with their default names (Figure 8). A student may click on the New button of the Light List window to create a new light. Once a light is listed, click on Remove to deactivate (i.e., turning it off), Active to activate, and Modify to modify a light.

Figure 8. The Light List window.


GraphicsMentor supports two types of light source, point light (default) and spot light. A point light is represented by a dot in all four subwindows and shown in the color of the light. Except for the default light 0, whose initial position is above the coordinate origin, all other lights have their initial positions at the origin. A click on the Modify button of the Light List window brings up a light window of the selected light (Figure 9(a)). The bottom part of this window shows the name, color and coordinates (i.e., position) of the light being modified. The upper-right corner buttons permit a student to switch between point light and spot light. The top three slides control the RGB components of the light color, and the three buttons to the right of the slides allow a student to choose one of the ambient, diffuse, and specular components to modify.

Figure 9. . A point light source.
(a) A point light window
(b) a problem


Once a light is selected, a student can left-drag it to a new position in any side-view subwindow. Thus, combined with the camera and material property of each object, a student can experiment and verify many important concepts and effects of an illumination/lighting model. A must-show example illustrates two of the most important drawbacks of local illumination models: no shadows and non-blocking light. Figure 9(b) shows a big yellow oblate ellipsoid between the light source (i.e., the white dot) and a small red sphere. Note that the light source is very close to the oblate ellipsoid. It is clear that the light cannot illuminate the sphere in reality; however, the image clearly shows that the portion of the red sphere facing the light is illuminated and the oblate ellipsoid casts no shadow on the red sphere!

GraphicsMentor also supports spot lights. A click on the Modify button of a light source brings up its light window. Then, click on the Spot Light button of the selected light window changes the light to a spot light (Figure 10(a)). In fact, the spot light window is identical to the point light version, except that there are five more slides for modifying the characteristics of a spot light. The spot light icon, as shown in the Canvas window, is a dot with a cone attached shown in the color of the light. A student may left-drag the spot light icon to change its position, and right-drag to modify the light direction. The top three slides are for modifying the coefficients kc, kl and kq of the attenuation factor, which is the reciprocal of kc + kl d + kq d2, where d is the distance between an object and a spot light. The Spot Exponent slide controls the concentration of the spot light, and the Cutoff Angle slide controls the spot light cone angle.

Figure 10. Spot lights.
(a) A spot light window
(b) Color mixing


An interesting experiment for students to do is to visualize a mix of colored lights (Figure 10(b)). A thin white box is placed in the scene along with three spot lights with colors red, green and blue, respectively, each of which has a small cutoff angle so that it can only illuminate the vicinity of the coordinate origin. The camera is placed above the origin. A student can choose different position, color, cutoff angle, spot exponent of a spot light to generate different effects. In this way, an instructor may be able to cover some color models easily.

GraphicsMentor is also useful in helping students visualize other shortcomings of local illumination models. An oblate ellipsoid with coarse triangulation (for demonstrating the relationship between coarse triangulation and spot light) is placed in the scene (Figure 11(a)). There are two lights. The top one is a spot light of white color, placed close enough to the surface so that its light cone only covers a portion of the surface. The bottom one is a mid gray point light for illuminating the bottom part of the surface. The camera is placed above the surface. Because the triangulation is coarse, the spot light does not shed a circular shape on the surface. Instead, the shape is a polygon whose shape depends on the way of triangulating the surface. See the top view and world view subwindows. The silhouette of the surface in the Camera View window is barely seen, and the spot light generates a hexagonal illuminated area on the surface. The Mach band effect is clearly seen!

Figure 11 (a) and (b). The impact of tessellation on rendering.

6. Basic Animation
GraphicsMentor supports basic keyframe animation. A click on the Animation menu button of the Canvas window brings up the Animation Control window (Figure 12). Then, the characteristics of the camera, light sources, and objects may be altered. Once this is done, click on the Record button in the Animation Control window to record a keyframe. This process is repeated until all keyframes are recorded. Then, click the Play button to play, the Stop button to stop, and the Record button to append more keyframes. GraphicsMentor will take these keyframes, calculate the frame rate, and interpolate necessary frames between two adjacent keyframes.

Figure 12. Animation Control window.


Figure 13 shows a simple example. Three spheres, in yellow, red, and blue, rotate about the origin with camera pointing downward. Eight keyframes are recorded as shown. The yellow sphere rotates about 130 degree, the red one rotates about 180 degree and is a little faster, and the blue one rotates about 360 degree and is the fastest moving object. After all eight keyframes are recorded and click on the Play button, GraphicsMentor generates intermediate frames and plays the animation smoothly.

Figure 13. A simple example of eight keyframes.

7. Global Illumination Models
As mentioned in previous sections, GraphicsMentor only supports local illumination models through an API (i.e., OpenGL). An obvious drawback of this approach is that students do not have a chance to learn global illumination models. There are a number of possible ways to overcome this problem. Currently, GraphicsMentor is capable of exporting its scene to POV-Ray, a well-known ray tracing program. In this way, a student designs and tests his scene with GraphicsMentor based on a local illumination model. Then, this scene is exported to POV-Ray for ray tracing. As a result, a student can compare the results obtained with a local illumination model and a global illumination model.

While ray tracing is capable of producing realistic images, it does have some well-known drawbacks (Glassner 1989; Shirley, 2000). For example, most ray tracing systems trace rays from a camera rather than from light sources. As a result, typical ray tracing systems do not support diffuse reflection. The scene in Figure 14(a) consists of a box and a reflective sphere enclosed in a large box whose top face (i.e., ceiling) has a white light source. This only light source does not illuminate the ceiling at all, which is quite contrary to reality. It is also difficult for a ray tracing system to generate indirect illumination. Figure 14(b) shows two mirror walls and a light source to the right of the red sphere at the center. In reality, the two mirror walls reflect the light ray from the light source, creating two weak shadows of the red sphere. However, we only see one strong shadow from the only light source. In addition to these problems, due to the way of handling light rays, a typical ray tracing system will not be able to generate caustics.


Figure 14 (a) and (b). Two ray tracing problems.


Another popular global illumination model is radiosity, which is based on the theory of heat transfer (Cohen & Wallace, 1993; Sillion & Puech, 1994). Radiosity can produce indirect illumination, color bleeding, soft shadows and very realistic looking images. However, in addition to being very time consuming, radiosity cannot handle reflection and refraction and every object must be triangulated. Note that radiosity may be incorporated into a ray tracing system (Larson and Shakespeare, 1997; POV-Ray, 2002). Photon mapping is a very interesting approach developed in recent years that is efficient and capable of producing radiosity effects along with others (Jensen, 2001). With photon mapping, photons are shot from each light source and reflected from the hit objects until the energy diminishes to zero or the level of reflection reaches a pre-specified limit. Therefore, each photon carries the color and intensity of a light source and the color at the point of a hit object to other objects. This information is stored in a data structure called photon-map and is used to modify the ray traced result. In this way, photon mapping is able to generate many radiosity effects (e.g., color bleeding and soft shadow) and retain the advantages of ray tracing (e.g., reflection and refraction). Moreover, photon-mapping is also capable of creating some effects which are very difficult to do with ray tracing and radiosity (e.g., caustics). Figure 15 shows the effect of adding photon mapping to the scene in Figure 14(a). This image clearly shows some radiosity effects of color bleeding, indirect illumination of the ceiling, and soft shadows.

Figure 15. An image produced with photon mapping.

8. Future Work
The goal of this first stage development of GraphicsMentor is to design a usable prototype to help students learn the fundamentals. As a result, many important concepts are not supported fully, and will be added in the future. The following list will be included in the future development of GraphicsMentor. First, the object module will be improved to include more primitives such as superquadrics, B-spline and NURBS. Second, the current simple hierarchical modeling capability will be extended to support more sophisticated modeling activities and basic inverse-kinematic animation. Third, elementary texture mapping will be made available. Fourth, while GraphicsMentor does not support global illumination models directly, it can export a scene to POV-Ray for ray tracing so that a student can compare the differences between local and global illumination models. We are currently developing a small ray tracer that also supports photon mapping, and hope that eventually ray tracing and photon mapping will become available in GraphicsMentor. (In fact, Figure 15 was produced with our photon mapping system). A stand-alone radiosity system is also under development. Fifth, in addition to inverse-kinematics, the animation module will be expanded to include basic non-linear editing so that a student can design multiple animation sequences and join them together into a single stream. Sixth, since digital image editing has become a household tool due to the popularity of digital cameras and camcorders, it would be useful for GraphicsMentor to support a few basic postprocessing filters (e.g., motion and Gaussian blur, sharpening, and morphing). Seventh, we intend to make GraphicsMentor more modularized so that an instructor can select a component of GraphicsMentor for students to modify, extend, or even re-implement. In this way, students will have a better platform to practice graphics programming.

9. Conclusions
We have presented a pedagogical tool, GraphicsMentor, for teaching and learning the fundamentals of computer graphics. It compensates the ray tracing approach that has been used in our Introduction to Computing with Geometry course (Lowther and Shene, 2001) for helping students who do not have a graphics background quickly learn basic graphics concepts. GraphicsMentor can certainly be used in an introduction to computer graphics course to illustrate and demonstrate various concepts and algorithms. While there are numerous Java appelets available on the Internet that may serve the same purpose, we believe a stand-alone approach is superior because it can integrate many components into a single, uniform interface and yet perform efficiently. We plan to continually develop GraphicsMentor into a full-blown system in the near future. The interested readers may find more about our work, software availability, and future announcement at the following site: http://www.cs.mtu.edu/~shene/NSF-2
An external link to the author's web site for more about GraphicsMentor, software availability, and future announcement.

10. Acknowledgment
This is a revised and extended version of (Nikolic and Shene, 2002). This work was supported by the National Science Foundation under grants DUE-9653244, DUE-9952621 and DUE-0127401.

11. References
Cohen, M. F. and Wallace, J. R. (1993). Radiosity and Realistic Image Synthesis, Academic Press.

Glassner, A. S. editor (1989). An Introduction to Ray Tracing, Academic Press.

Jensen, H. W. (2001). Realistic Image Synthesis Using Photon Mappings, A K Peters.

Larson, G. W. and Shakespeare, R. (1997). Rendering with Radiance, Morgan Kaufmann.

Lowther, J. and Shene, C.-K. (2000). Rendering + Modeling + Animation + Postprocessing = Computer Graphics, The Journal of Computing in Small Colleges, 16 (1), 20-28. Reprinted in Computer Graphics, 34 (4), 15--18.

Lowther, J. and Shene, C.-K. (2001). Computing with Geometry as an Undergraduate Course: A Three-Year Experience, ACM 32nd SIGCSE Technical Symposium, February 21-25, 2001, 119-123.

Nikolic, D. and Shene, C.-K. (2002). GraphicsMentor: A Tool for Learning Graphics Fundamentals, ACM 33rd SIGCSE Technical Symposium, February 27 – March 3, 2002, 242-246.

POV-Ray (2002). Persistent of Vision - ray tracing system. Available free at http://www.povray.org/.

Shene, C.-K. (2002). Raytracing as a Tool for Learning Computer Graphics, to appear in ASEE/IEEE Frontiers in Education, November, 2002.

Shirley, P. (2000). Realistic Ray Tracing, A K Peters.

Sillion, F. X. and Puech, C. (1994). Radiosity and Global Illumination, Morgan Kaufmann.


********** End of Document **********
MEJ multimedia team member assigned to this paper Yue-Ling Wong